主な研究テーマ
理論と計算であらゆる化学現象を正確に予言出来るなら、何らかの形で射影された情報を眺める実験研究よりもはるかに詳細な情報を与える理論研究の価値は計り知れません。非経験的分子軌道理論は大きな成功を収めてきましたが、いまだ全ての研究分野で計算機実験が完全に先導するという所までは至っていません。分子科学にブレークスルーをもたらす斬新な理論と計算手法の開発が研究グループのテーマです。
スケーラブルな分子軌道理論
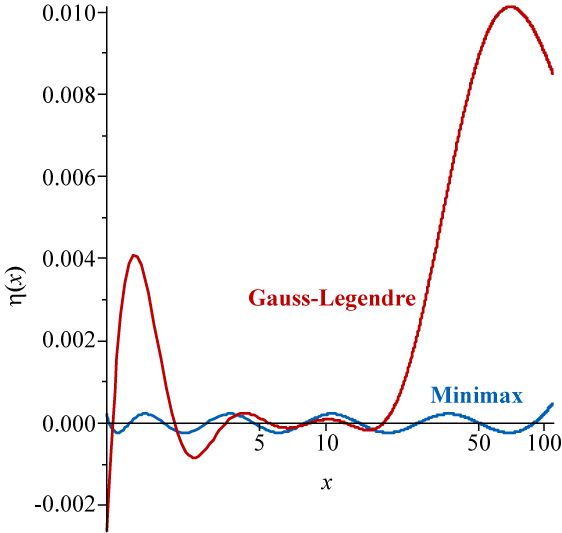
分子軌道理論は気相の原子や分子といった少数多体系を取り扱うのに強力な手法です。一方、その計算時間は系の大きさに対し式の上では4乗から6乗、ときにはそれ以上の次数で大きくなります。そのような次数を出来るだけ小さくして大規模分子軌道計算を可能にするスケーラブルな手法を開発は重要な課題です。私たちは分子軌道計算の相互作用積分の中で最も大きなデータ量となる、二電子反発積分の高速な計算手法や近似的分解法を研究して来ました。又、ミニマックス近似を大規模計算のためのラプラス変換したMP摂動理論に導入しました。これらの手法は、多体摂動論と結合クラスター理論からなる各種ハイブリッド法へ応用されています。
超高精度計算のための露わに電子相関を考慮した分子軌道理論の開発
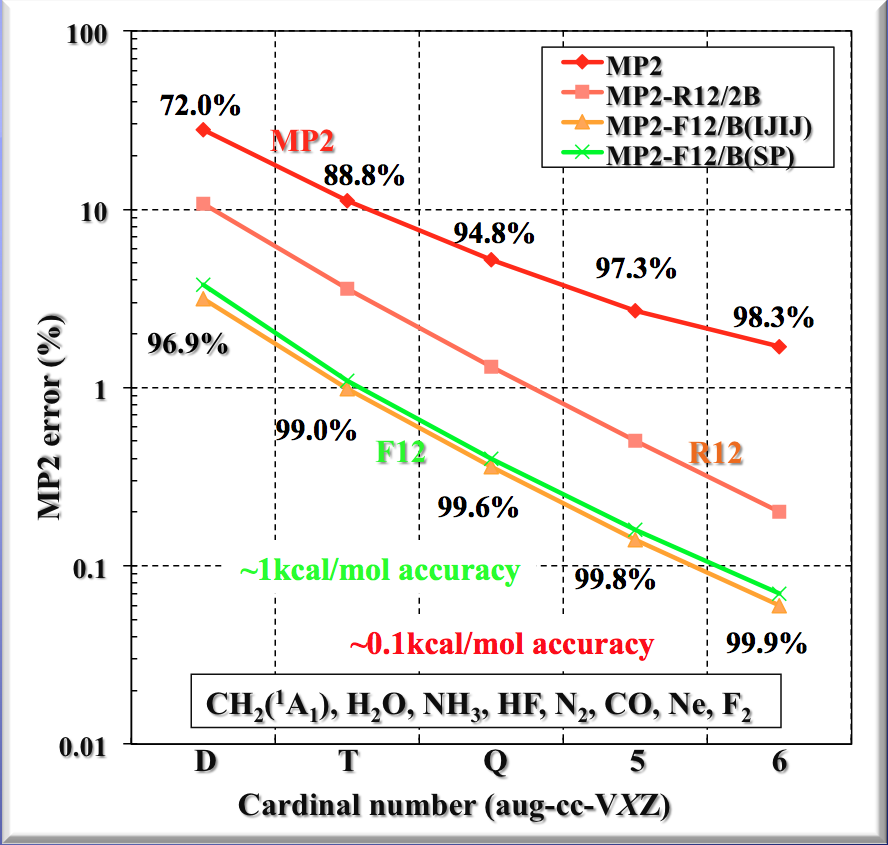
配置換相互作用(CI)展開の収束の遅さが物質の高精度計算で大きな障害の一つとなっています。通常の一電子描像に基づく分子軌道法は電子相関に対する収束が遅く、信頼できる結果を得るためには非常に大きな基底関数を用いる必要があります。この問題に対し我々は、カスプ条件に対する論理推進演算子と露わに電子間距離を含むスレーター型ジェミナルを用いたF12理論の開発を行って来ました。F12電子状態理論は、各種摂動法、CI展開、結合クラスター理論へと応用され、高精度量子化学計算の標準的手段に発展しています。さらに、F12の寄与を有効ハミルトニアンにした射影トランスコリレーション法をを用いた強相関物質の計算や量子コンピュータ向けの高精度な量子ビットハミルトニアンの構築を行っています。
モデル空間量子モンテカルロ法
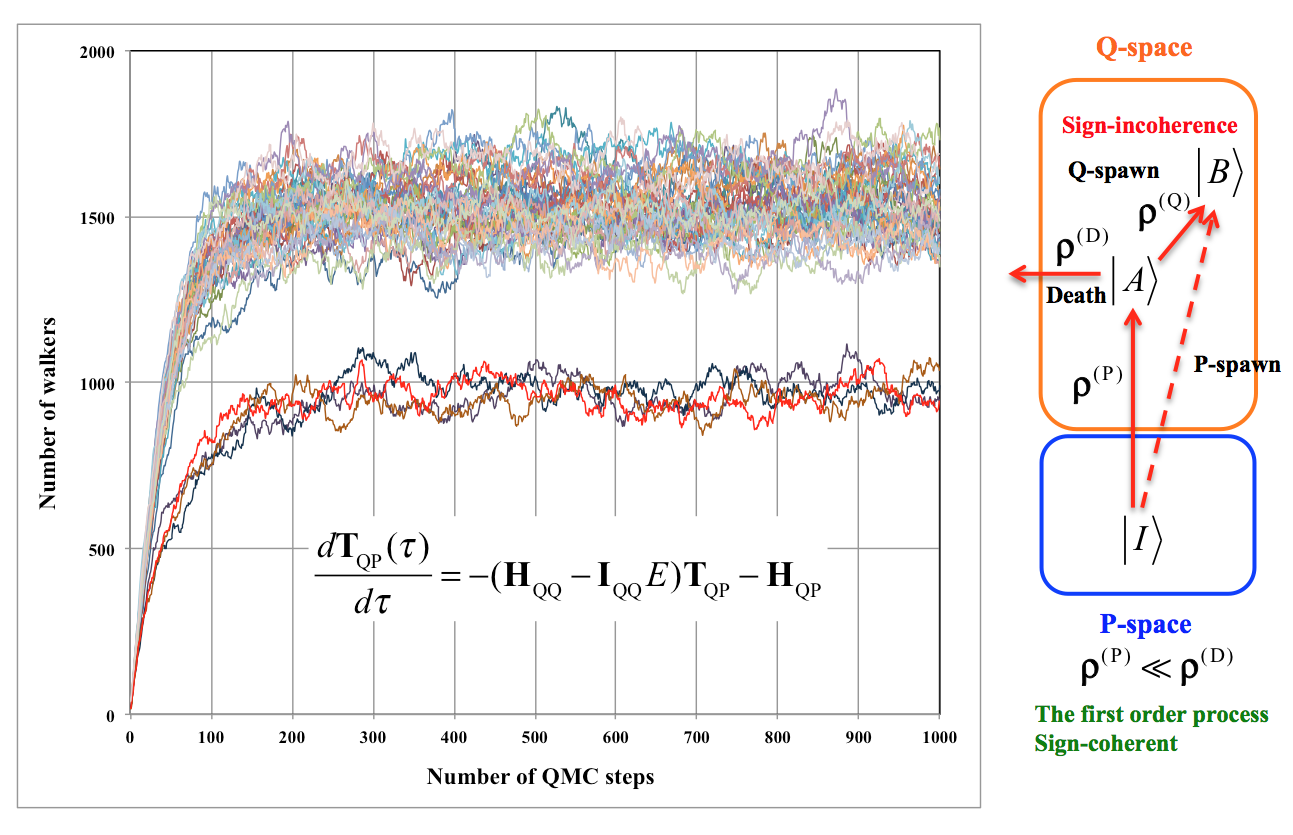
モデル空間量子モンテカルロ(MSQMC)法は、エネルギー依存した有効ハミルトニアンのトランスファー行列を確率過程によってサンプルする斬新な電子状態計算手法です。決定論と確率論を融合する事により、システムサイズに対して指数関数的に増加する完全CIの問題について、負符号問題を避けつつ量子状態がエネルギー的に近接している擬縮重状態や任意の励起状態の取り扱いが可能にしています。従来の分子軌道理論では定性的な予測すら困難であった電子状態の高精度計算を実現するMSQMC法の有用なソフトウエア開発を行うと共に、高電子励起状態や生物無機化学での多核金属錯体への応用を進めています。
強相関電子系のための完全結合クラスター展開
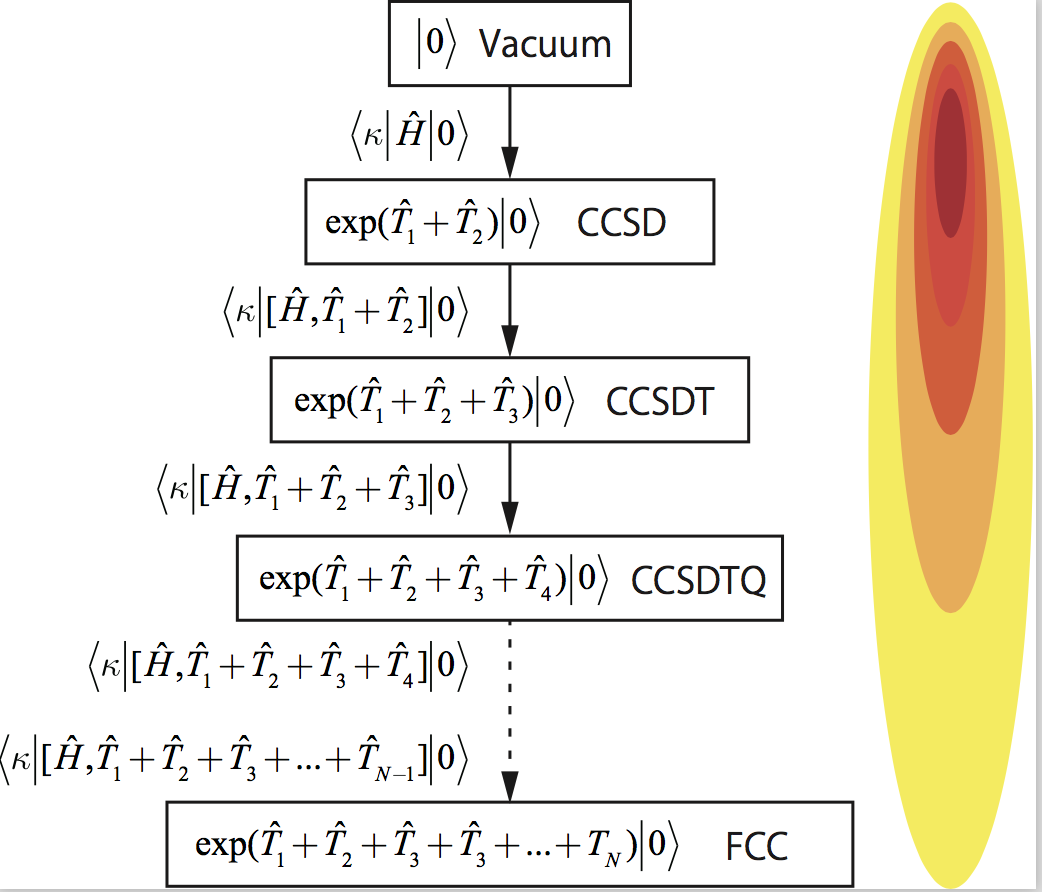
電子相関の強い物質の正確な理論的取り扱いは、従来の電子状態理論を超えた重要な応用分野をもたらす事が期待されます。この目的で、近年、統計論や決定論を用いた選択的CI法の研究が発達して来ていますが、CI展開は系の大きさに対し指数関数的に展開が複雑化する事から応用範囲が大きく限定されます。我々は、完全な指数関数型の波動関数を用いる完全結合クラスター展開(FCC)から出発し、クラスター演算子とその積が疎であるという性質を用いた完全結合クラスター還元法(FCCR)を開発しました。FCCR法は電子の動的相関と静的相関を同時に取り扱う事が出来、多核遷移金属錯体や高温超伝導物質の正確な物質設計を可能にすると期待されています。
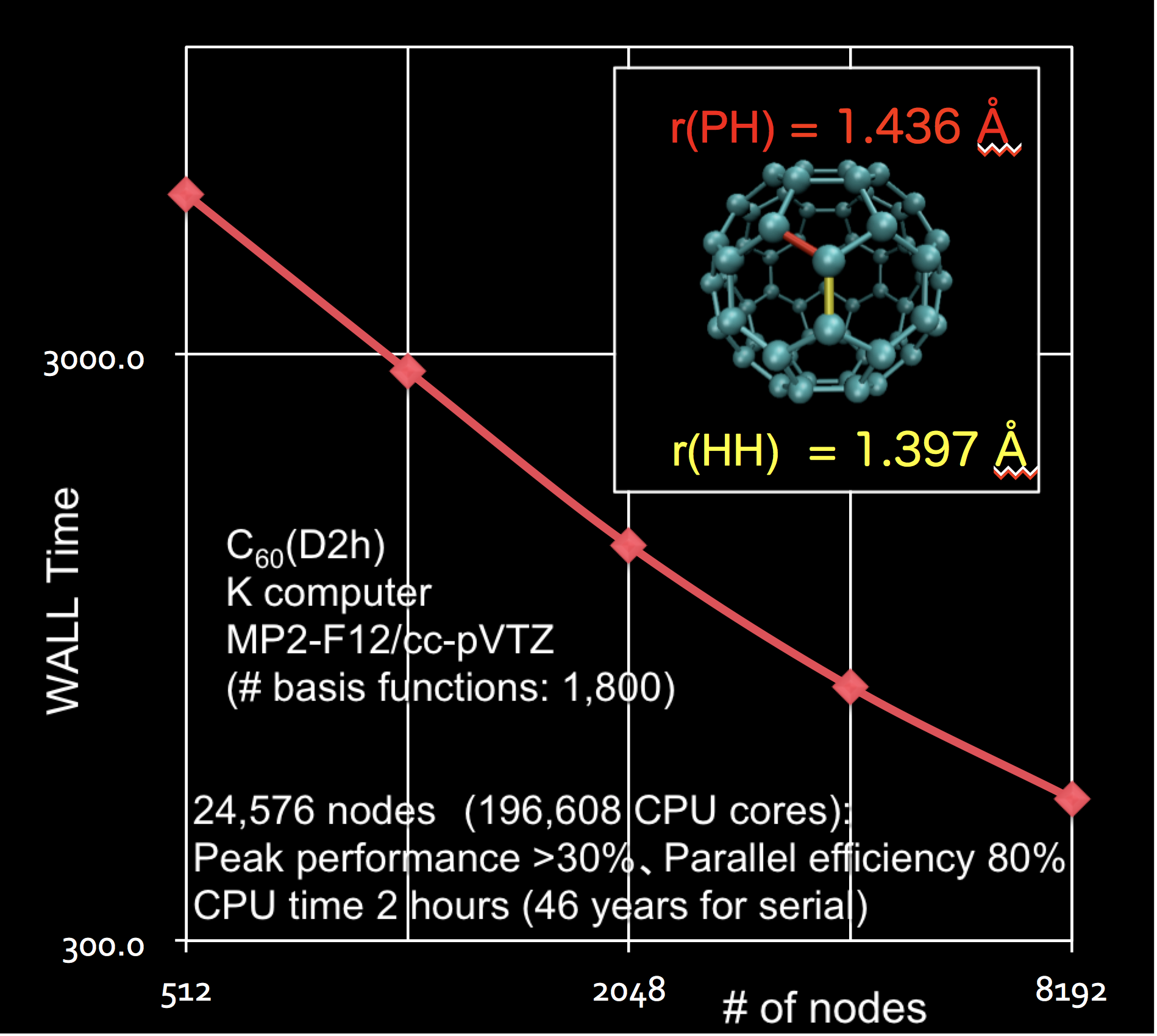
超並列計算アルゴリズムの開発とプログラム高度生成
ハイパフォーマンス計算では超並列環境の高度利用が急速に進んでおり、応用計算で用いられるコア数は急激に増加してきました。これに従って、精度や空間スケール、時間スケールで、これまでと本質的に異なる成果をもたらす計算科学のパラダイムシフトが要求されます。MPIやOpenMPを用いて、数十万CPUコアの超並列環境に対応した計算手法とアルゴリズムの開発を行い、主に超並列コンピュータでの応用研究を行っています。又、物質科学で用いられる計算手法は極めて複雑化しており、基本方程式からソースコードを自動生成する技術が発展しています。数式の整数表現を元に演算子の並べ替えを含む最適化や自動チューニングを考慮に入れた研究を行なっています。
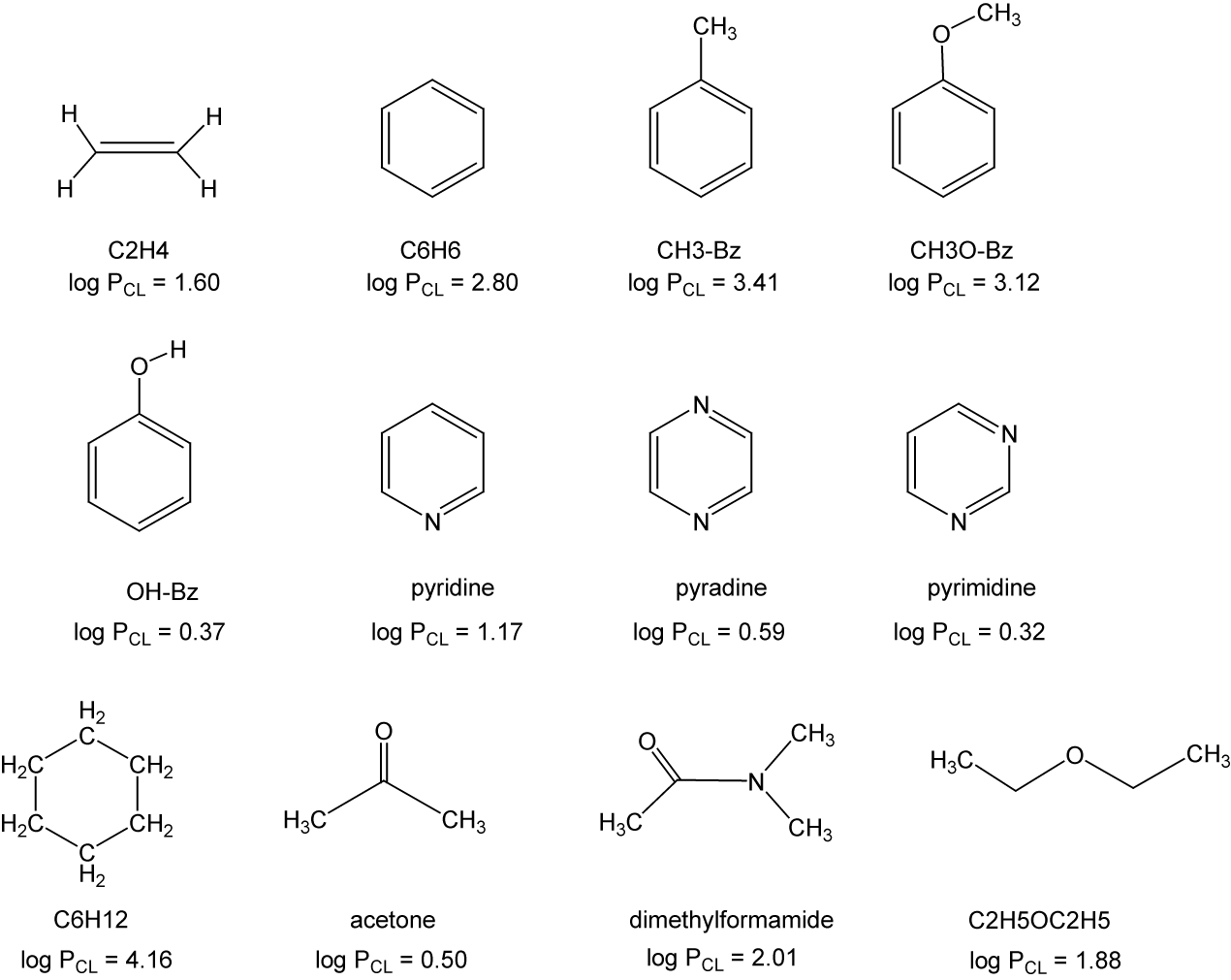
溶液中の電子状態理論
工業的に重要な殆どの化学反応は溶液中で進行するため、化学反応に対する溶媒効果は極めて重要性な研究テーマです。私たちは、拡張 RISM理論を初めて分子軌道法の分野に適用し、高速かつ分子論的な溶媒効果を含む量子化学的手法を発展させました。更に拡張RISM理論は近似の不透明さとサイト間の球対称ポテンシャル関数という制約取り除くために、分子Ornstein-Zernike方程式を部分波展開した新しいタイプの積分方程式理論を提案しました。角度依存性を含む完全な分子内相関関数を導入することにより、本来距離幾何情報だけからは得られるはずのないキラルな分子の相互作用等を矛盾無く説明できる理論の枠組みを作りました。この理論から導かれた溶媒和自由エネルギー表式は分配係数の計算に応用されています。
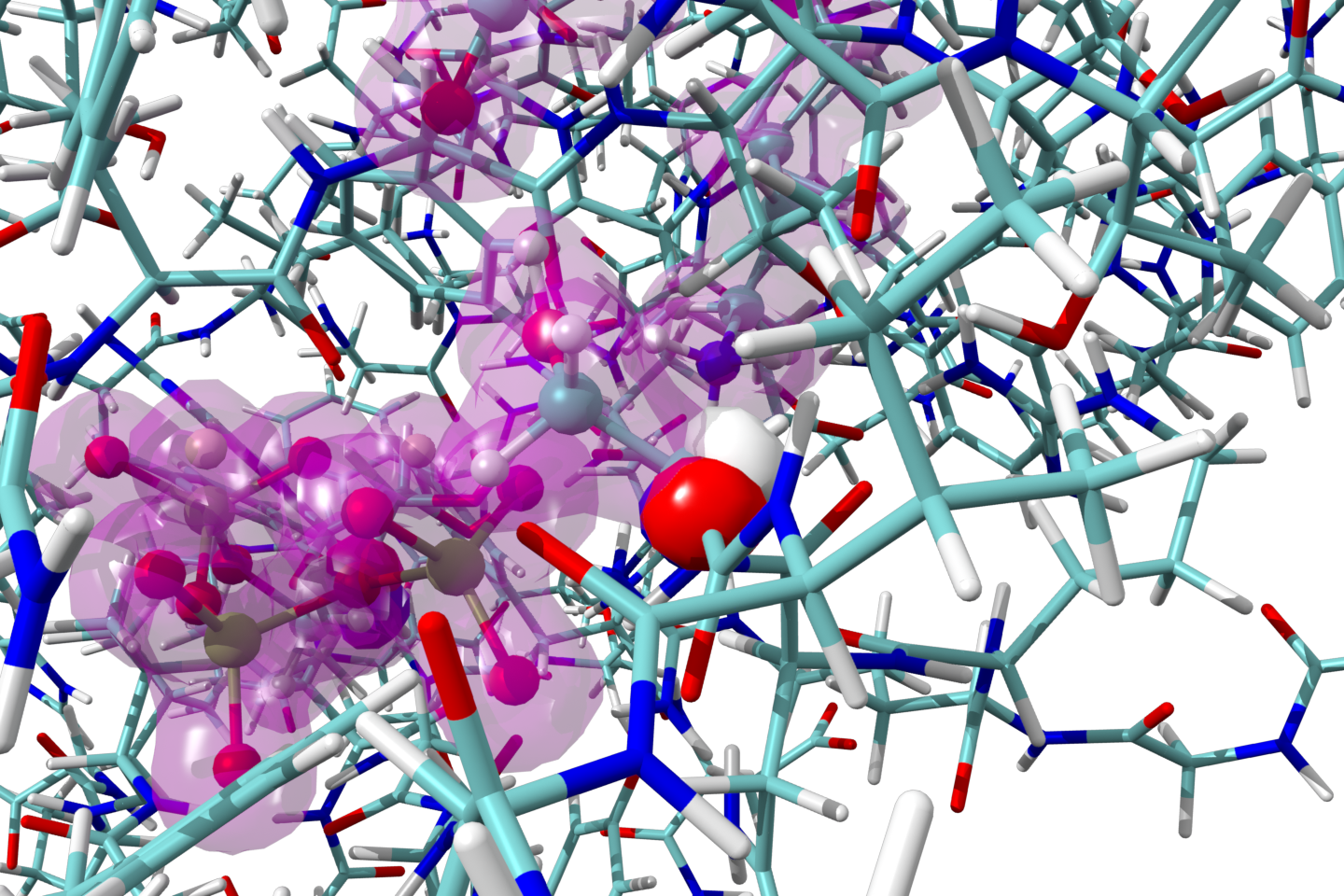
新規マルチスケールモデルの開発
量子力学と分子力学を折衷したマルチスケールモデル(QM/MM法)は酵素や溶媒の存在下での化学反応を取り扱うのに強力な方法です。我々は、連結原子を含まない、一般化混成軌道(GHO)QM/MM法を補助軌道に関する等電荷と直交化法を用いて拡張してきました。この方法はPKA(c-AMP dependent protein kinase)やその他の酵素反応に応用されています。又、境界原子周りの幾何構造を正確に再現する制限付き混成行列を用いたGHO-MP2エネルギー勾配法に基づくQM/MM分子動力学法の開発も行っており、蛋白質のNMR遮蔽テンソルやCDスペクトルの研究に応用されています。
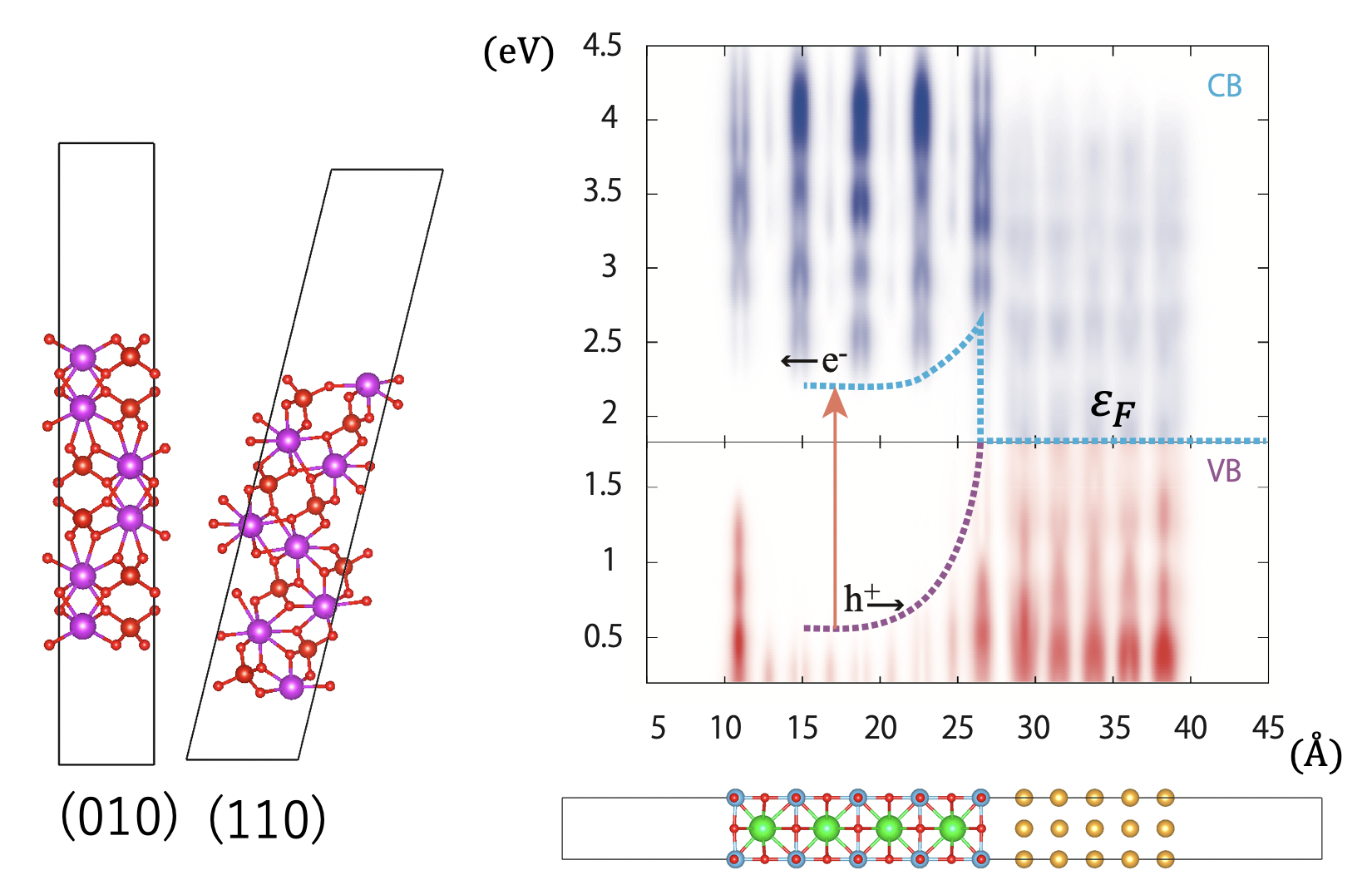
半導体光触媒の研究
光エネルギーを化学エネルギーに変換する光触媒(人工光合成)の高効率化には、光応答や電荷分離などの条件が複雑に関係しています。半導体表面や、固-固界面(半導体/半導体、半導体/助触媒、半導体/メディエーター)のバンド曲がりやショットキー障壁の計算に基づき、吸光やキャリア特性に優れた光触媒のメカニズムと材料の研究を行っています。また、逐次的な光吸収に伴う水の酸化還元反応の中間体の構造やスピン状態を解析することにより反応機構解明に取り組んでいます。得られた支配要因の知見を元に新規の光触媒・助触媒の材料設計を目指します。
GELLAN量子化学プログラムの開発
超並列・階層的量子化学計算プログラムGELLANの開発を行っています。研究室のこれまでの研究成果の蓄積と更なる開発、応用計算を行うためのプラットフォームです。リクエストに応じたバイナリー配布です。